Induktionsgesetz
Herleitung
Bei einem Gleichstromgenerator bewegt man einen Leiter in einem konstanten Magnetfeld. Die induzierte Spannung berechnet man nach dem Induktionsgesetz.
$$ U=v\cdot B\cdot l\cdot z$$
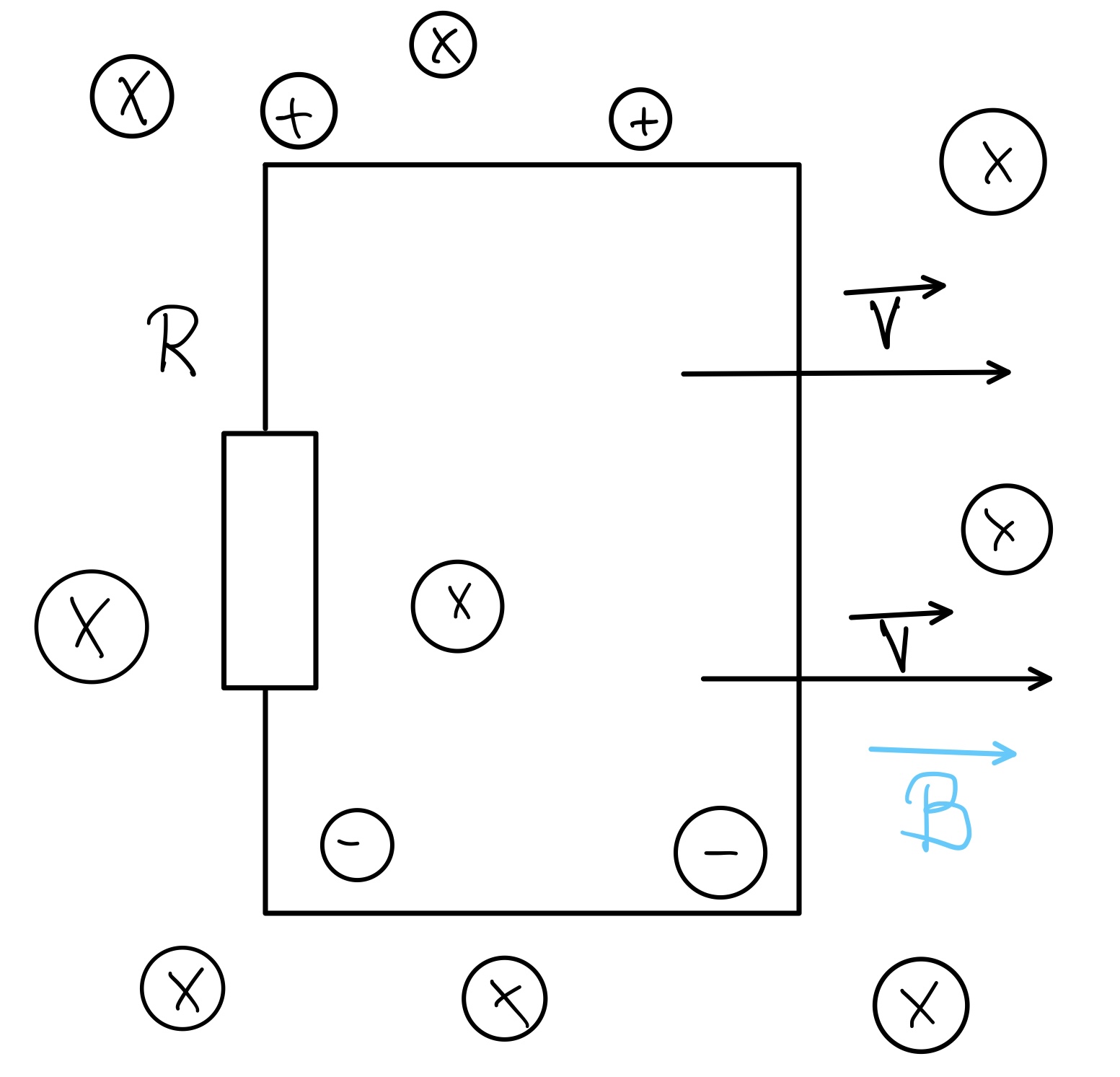
Bewegt man einen Leiter so in einem Magnetfeld, dass er die Feldlinien schneidet, so wird in dem Leiter
eine Spannung induziert, die man mit folgender Formel berechnet:
$$ U=v\cdot B\cdot l\cdot z$$
ZEICHNUNG FEHLT
Bei einer Geschwindigkeit v let die Leiterschleife in einer bestimmten Zeit Δt eine bestimmte Strecke Δx
innerhalb des Magnetfeldes zurück, dabei gilt mit:
$$v=\frac{\Delta x}{\Delta t} $$
$$U=\frac{\Delta x}{\Delta t} \cdot B\cdot l$$
Bei einer Geschwindigkeit v überstreicht die Leiterschleife in einer bestimmten Zeit Δt eine bestimmte
Fläche ΔA innerhalb des Magnetfeldes:
Die Fläche ΔA berechnet sich dabei nach der Formel:
$$\Delta A=I\cdot \Delta x$$
$$U=\frac{\Delta A}{\Delta t} \cdot B$$
Diese Flächenänderung innerhalb der Leiterschleife, bewirkt zusammen mit der magnetischen
Flussdichte B eine Flussänderung ΔΦ.
$$\Delta \Phi =B\cdot \Delta A$$
Man erhält:
$$ U=\frac{\Delta \Phi }{\Delta t} $$
Wird die Leiterschleife (eine einzige Windung) durch eine Spule mit N Windungen ersetzt, so ergibt sich die N-fache Induktionsspannung.
$$U=N\cdot \frac{\Delta \Phi }{\Delta t} $$
Wenn die Leiterschleife in das Magnetfeld hineinbewegt wird, die Flussänderung positiv ist, so wird eine
negative Spannung induziert.
Wen die Leiterschleife aus dem Magnetfeld hinausbewegt wird, die Flussänderung negativ ist, so wird
eine positive Spannung induziert.
Dieses Verhalten berücksichtigt man in der Formel indem man in Minuszeichen hinzufügt.
$$U=-N\cdot \frac{\Delta \Phi }{\Delta t} $$
Merke:
Man kann eine Spannung erzeugen,
indem man einen Leiter in einem konstanten Magnetfeld bewegt, oder
bei einem in einem Magnetfeld ruhenden Leiter das Magnetfeld verändern.
$$ U=v\cdot B\cdot l\cdot z$$
$$U=-N\cdot \frac{\Delta \Phi }{\Delta t} $$